1月に組み分けテストも終わったらすぐに復習テスト
三年生も忙しくなってきました
SAPIXの算数の範囲を確認していたところ
「正方形に人が並んでいる問題」が出てきました。
息子(小3)がこれで大苦戦。
私も最初、「え?何が難しいの?」と思ったんですが、よく見ると大人でもハマる罠がありました!
今日は、この「正方形の並び方」問題について、なぜ小3のこの時期に出るのか、中学受験ではどう使われるのか、そして数学的に何を学んでいるのかをママ目線で整理してみます。
まず、どんな問題?
こんな感じです:
問題例:
正方形の形に人が並んでいます。一辺に5人並んでいます。全部で何人並んでいますか?
パッと見ると簡単そうですよね。でも、息子の答えは…
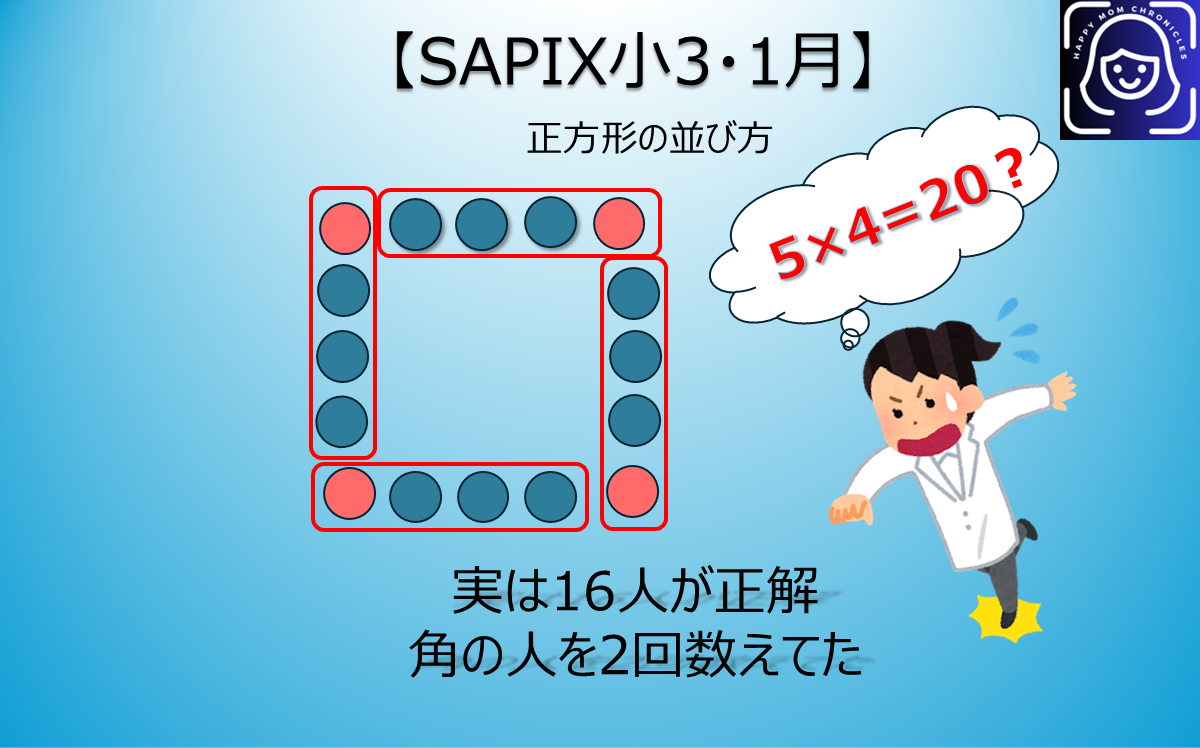
「5 × 4 = 20人!」
これ、実は不正解なんです。
なぜ「5×4=20」がダメなのか
図を描いてみると分かります:
👤 👤 👤 👤 👤
👤 👤
👤 👤
👤 👤
👤 👤 👤 👤 👤
角の人(👤)は、2つの辺に属しています。
- 上の辺:5人
- 右の辺:5人
- 下の辺:5人
- 左の辺:5人
単純に 5 × 4 = 20 と計算すると、角の4人を2回数えてしまうんです。
正しくは: 5 × 4 – 4 = 16人
または
(5 – 1) × 4 = 16人
なぜ小3の1月(新小4直前)に出題されるのか
SAPIXでは「方陣算」という名称は使いませんが、この時期にこの問題が出る理由があります。
1. かけ算の理解度チェック
小3の前半でかけ算を習います。でも、「5×4」と暗記するだけでは不十分。
この問題は:
- かけ算が「本当の意味」で理解できているか
- 式を立てる前に「何を数えるべきか」考えられるか
をチェックしています。
2. 図形センスの土台
中学受験の算数では、図形を見て情報を整理する力が必須です。
この問題で学ぶのは:
- 重複を見抜く目
- 図を描いて考える習慣
- 見えないものを可視化する力
3. 論理的思考の訓練
「なんとなく」ではなく、なぜその式になるのか説明できることが大切。
息子は最初、「だって5人が4つあるから20でしょ?」と言いました。でも、図を見せると「あ!角の人が…」と気づきました。
中学受験ではどう出題されるか
この「正方形の並び方」問題、実は中学受験の頻出パターンです。
応用例1:中空の正方形
正方形に人が並んでいます。外側の一辺に10人、内側の一辺に6人並んでいます。全部で何人ですか?
外側と内側の差を求める問題。
解き方:
- 外側:10 × 4 – 4 = 36人
- 内側:6 × 4 – 4 = 20人
- 答え:36 – 20 = 16人
応用例2:逆算
正方形に全部で32人並んでいます。一辺には何人並んでいますか?
これは逆向きの思考が必要。
解き方:
- 32 + 4 = 36
- 36 ÷ 4 = 9人
応用例3:長方形への応用
長方形に人が並んでいます。長い辺に8人、短い辺に5人並んでいます…
正方形で学んだ「角の重複」の考え方を、長方形に応用します。
数学的に何を学んでいるのか?
実は、この問題は高校数学の「集合」とベン図につながっています。
ベン図で考えると分かりやすい!
正方形の各辺を集合として考えてみましょう:
A = 上の辺にいる人たち
B = 右の辺にいる人たち
C = 下の辺にいる人たち
D = 左の辺にいる人たち
全体の人数は? → A + B + C + D をしたいところですが…
問題:角の人が重複している!
- 右上の角:AとBの両方に入っている(A∩B)
- 右下の角:BとCの両方に入っている(B∩C)
- 左下の角:CとDの両方に入っている(C∩D)
- 左上の角:DとAの両方に入っている(D∩A)
だから:
全体 = A + B + C + D - 重複分
= A + B + C + D - 4(角の4人)
包除原理(Inclusion-Exclusion Principle)
これが高校数学で習う「和集合の公式」です:
|A∪B| = |A| + |B| – |A∩B|
(読み方:Aの個数 + Bの個数 – 共通部分の個数)
例:一辺5人の場合
- 上の辺(A):5人
- 右の辺(B):5人
- 下の辺(C):5人
- 左の辺(D):5人
- 角(共通部分):4人
→ 5 + 5 + 5 + 5 – 4 = 16人
つまり、小3で「ベン図の基礎」を学んでいる!
- 重複を見抜く力 → データ分析の基礎
- 集合の考え方 → プログラミングの基礎
- 場合の数 → 確率・統計の基礎
「正方形に人が並んでいる」という身近な問題から、子どもたちは知らず知らずのうちに、データサイエンスの基礎まで学んでいるんです。
中学・高校でどう使う?
中1数学: 集合(ベン図)
- 「サッカー部とバスケ部、両方に入っている人は?」
- まさに方陣算と同じ考え方!
高校数学: 確率・場合の数
- 「AまたはBが起こる確率」
- 包除原理を使って計算
大学・社会: データ分析
- 「商品AとBを両方買った顧客は?」
- SQLクエリでもこの考え方を使います
小3で学ぶこの問題、実は算数→数学→データサイエンスへと続く重要な第一歩なんです。
ママ目線:どうサポートする?
息子がこの問題でつまずいたとき、私がやったことです。
1. 実際に並んでみた
リビングにマスキングテープで正方形を作り、家族4人で角に立ってみました。
「お母さんは上の辺と左の辺、両方にいるよね?」
これで一発で理解しました。
2. 絵を描かせる
式を書く前に、必ず図を描かせます。
- 〇で人を表す
- 角の人を赤で囲む
視覚化することで、「なぜ-4が必要か」が腹落ちします。
3. 3つの解法を見せる
一辺5人の場合、答えは16人。計算方法は3つあります:
方法1:各辺から片方の角を除く
(一辺 - 1) × 4
(5 - 1) × 4 = 4 × 4 = 16人
考え方:各辺5人のうち、片方の角だけ除いた4人を4辺分
方法2:全部数えて重複を引く
一辺 × 4 - 4
5 × 4 - 4 = 20 - 4 = 16人
考え方:全部数えたら20人、でも角4人を2回数えてるから引く
方法3:各辺から両端の角を除いて、角を最後に足す
(一辺 - 2) × 4 + 4
(5 - 2) × 4 + 4 = 3 × 4 + 4 = 12 + 4 = 16人
考え方:各辺から両端の角を除いた3人を4辺分、最後に角4人を足す
どれを使ってもOK。息子は「方法2(全部数えて引く)」が分かりやすいと言っています。
4. よくある間違いを先に見せる
「5×4=20って答える子が多いんだって。なんでダメだと思う?」
先に間違いパターンを見せることで、同じ間違いをしにくくなります。
練習のコツ
スモールステップで
- まず一辺3〜5人で練習
- 図が描きやすい
- 暗算できる
- 次に一辺10人くらいで
- 少し複雑になる
- でも考え方は同じ
- 中空の正方形に挑戦
- 外側と内側の差
- 応用力がつく
- 最後に逆算
- 「全部で○人、一辺は?」
- 本当に理解しているか確認
反復練習より理解優先
SAPIXの保護者会でも言われましたが、
この手の問題は反復練習より、1問をじっくり理解する方が効果的です。
「なんで-4するの?」が言えるようになったら、もう大丈夫…なはず!
まとめ:小3の1月は算数の分岐点
この「正方形の並び方」問題、実は小3算数の大きな分岐点だと感じています。
この問題ができる子は:
- かけ算を暗記ではなく理解している
- 図を描いて考える習慣がある
- 論理的に説明できる
つまずく子は:
- 公式暗記に頼っている
- 図を描く習慣がない
- 「なぜ」を考えていない
新小4(2月)からは、いよいよ本格的な受験算数が始まります。
この1月の「正方形の並び方」で、図形を見て考える力をしっかり身につけることが、4年生以降の算数を左右します。
追記:便利な練習ツール
息子のために、インタラクティブな練習ツールを作りました。
- 人数を変えられる
- 角の人がハイライト
- 3つの解法を比較
- クイズモード付き
ブログ読者の方にもシェアしますので、よかったら使ってみてください!
最後まで読んでいただき、ありがとうございました。
同じように「正方形の並び方」で悩んでいる方の参考になれば嬉しいです。
質問やコメントがあれば、お気軽にどうぞ!
タグ
#SAPIX #小3算数 #中学受験 #方陣算 #図形問題 #算数つまずきポイント #新小4準備
カテゴリ
中学受験 > 算数 > 小3 SAPIX > 学習サポート