「旅人算って何?」「なんで引き算したり、足し算したりするの?」
小学生の算数で出てくる旅人算。初めて聞くと難しそうに感じますが、実は図を描けば驚くほど簡単なんです。
旅人算とは、2人以上の人が移動するときの「速さ」「距離」「時間」を求める問題のこと。
この記事では、図解をたっぷり使って、旅人算の基本から応用まで、小学生でも分かるように徹底解説します!
📚 目次
旅人算とは?基本を理解しよう
旅人算(たびびとざん)とは、2人以上の人が移動するときの問題です。
求めるものは主に3つ:
- 速さ(何m/分で移動するか)
- 距離(どれだけ離れているか)
- 時間(何分後に追いつくか、出会うか)
旅人算は、「速さ × 時間 = 距離」という基本公式をベースに考えます。
💡 覚えておこう!速さの3公式
- 距離 = 速さ × 時間
- 速さ = 距離 ÷ 時間
- 時間 = 距離 ÷ 速さ
旅人算の5つのパターン
旅人算には、大きく分けて5つのパターンがあります。
| パターン | 説明 | 使う公式 |
|---|---|---|
| ①追いつき算 | 同じ方向に進んで追いつく | 速さの差 |
| ②出会い算 | 向かい合って進んで出会う | 速さの和 |
| ③反向算 | 同じ場所から反対方向へ | 速さの和 |
| ④円周上(同じ方向) | 円周を同じ向きに進む | 速さの差 |
| ⑤円周上(反対方向) | 円周を反対向きに進む | 速さの和 |
見分けるコツは、「同じ方向なら差、向かい合うなら和」です!
追いつき算の解き方【パターン①】
なぜ「速さの差」を使うの?
追いつき算は、同じ方向に進んで、速い人が遅い人を追いかける問題です。
📝 例題
A君は分速80m、B君は分速60mで同じ方向に進んでいます。
A君がB君の400m後ろからスタートすると、何分後に追いつきますか?
❌ よくある間違い
「400 ÷ 80 = 5分」と計算してしまう。
→ これはA君だけの速さで計算しているので間違いです!
⭕ 正しい考え方
追いかけっこをイメージしてください。
スタート時点: 🏃♂️A君(速い) ← 400m離れている → 🚶♂️B君(遅い) 1分後: 🏃♂️A君は80m進む 🚶♂️B君は60m進む → 距離は 80-60 = 20m 縮まる!
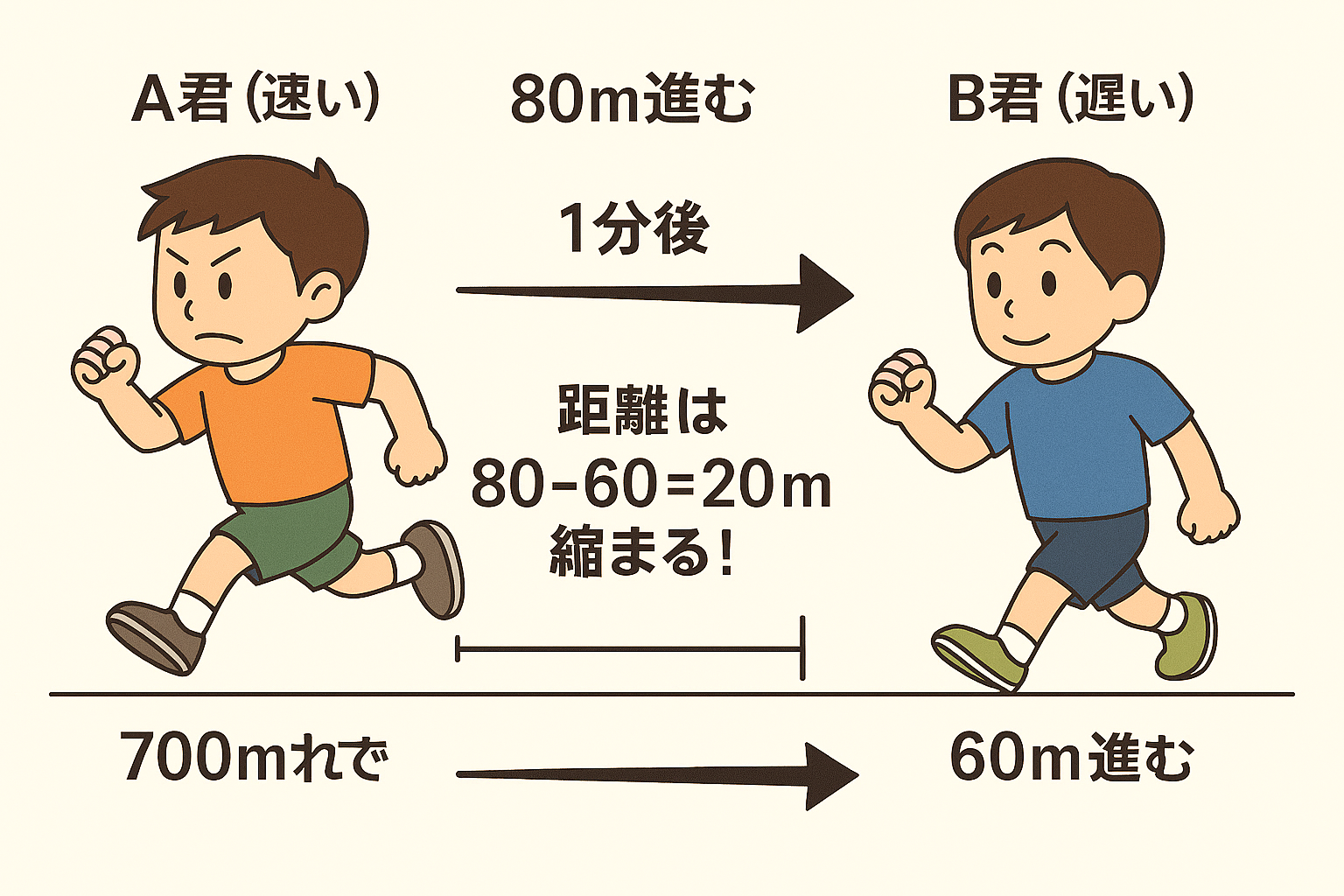
💡 速さの差で考える追いつき算!
A君は1分で80m、B君は60m進むから、1分ごとに20mずつ距離が縮まるよ
2人の距離が縮まる速さは:
速さの差 = 80 – 60 = 20m/分
400mの差を縮めるには:
400 ÷ 20 = 20分後
追いつき算の公式
追いつき算の公式
時間 = 距離 ÷ (速い人の速さ – 遅い人の速さ)
時間 = 距離 ÷ 速さの差
出会い算の解き方【パターン②】
なぜ「速さの和」を使うの?
出会い算は、向かい合って進んで、2人が出会う問題です。
📝 例題
1400m離れた2地点から、A君は分速80m、B君は分速60mで向かい合って進みます。
何分後に出会いますか?
📊 図で理解しよう
スタート時点: 🏃♂️A君 ← 1400m離れている → 🏃♀️B君 1分後: A君は右に80m進む → ← B君は左に60m進む 合わせて 80+60 = 140m 縮まる!
向かい合って進むので、2人の速さを足した速さで距離が縮まります。
速さの和 = 80 + 60 = 140m/分
1400mの距離が縮まるのは:
1400 ÷ 140 = 10分後
出会い算の公式
出会い算の公式
時間 = 距離 ÷ (A君の速さ + B君の速さ)
時間 = 距離 ÷ 速さの和
反向算の解き方【パターン③】
反向算は、同じ場所からスタートして、反対方向に進む問題です。
📝 例題
同じ地点からA君は分速80m、B君は分速60mで反対方向に進みます。
10分後、2人の間の距離は何mですか?
📊 図で理解しよう
スタート時点: 🏃♂️A君 📍 🏃♀️B君 10分後: 🏃♂️(左に800m) 📍 (右に600m)🏃♀️ 合わせて 800+600 = 1400m 離れている
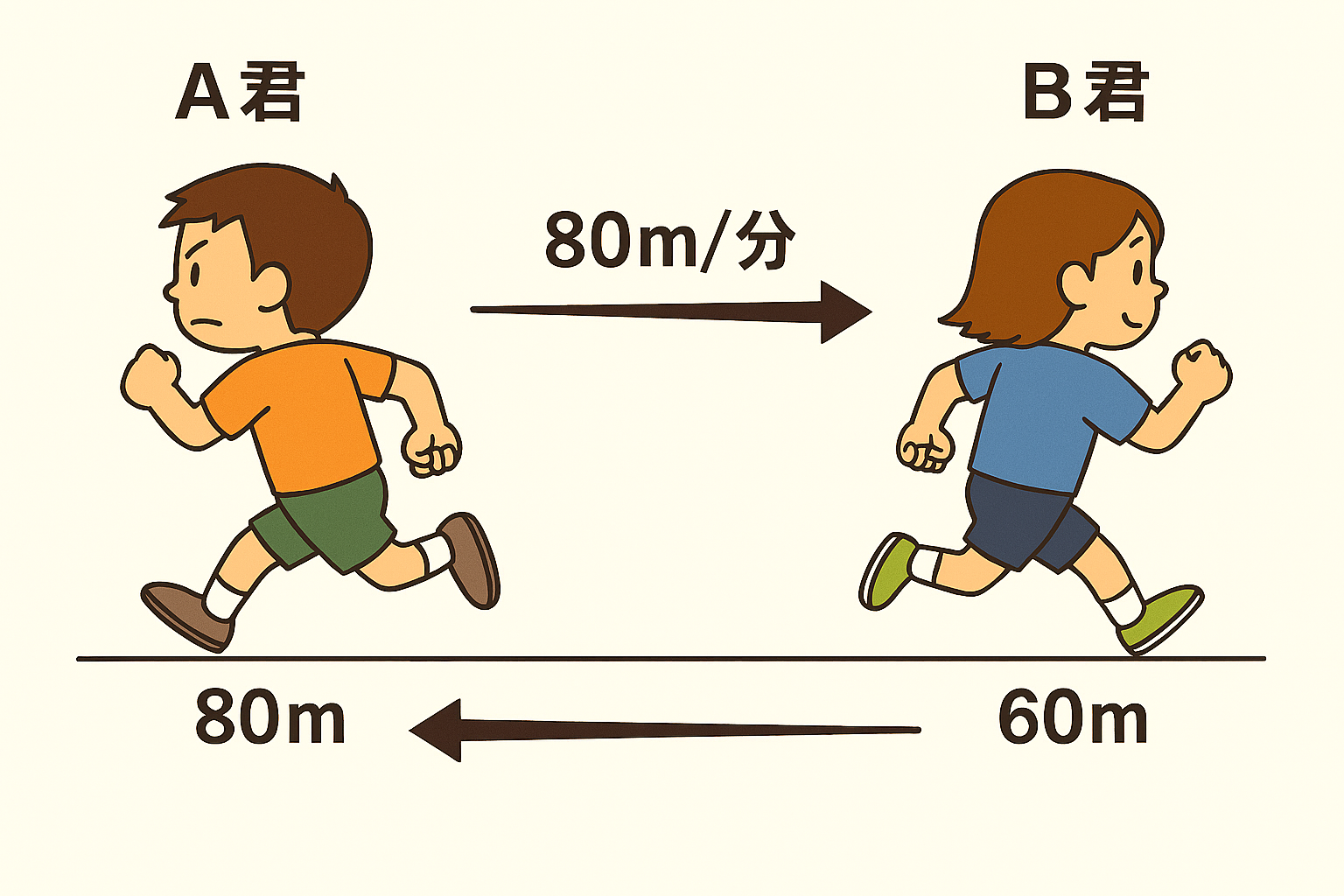
反対方向に進むので、2人が離れる速さは速さの和です。
速さの和 = 80 + 60 = 140m/分
10分後の距離は:
140 × 10 = 1400m
反向算の公式
距離 = (A君の速さ + B君の速さ)× 時間
距離 = 速さの和 × 時間
円周上(同じ方向)の解き方【パターン④】
円周上を同じ方向にぐるぐる回る問題です。
📝 例題
1周1200mの池の周りを、A君は分速80m、B君は分速60mで同じ方向に進みます。
次に出会うのは何分後ですか?
🤔 考え方のポイント
同じ方向に進むので、速い人が1周多く進んだときに追いつきます。
つまり、1200m(1周分)の差を縮めるのと同じです。
💡 「1周多く進む」ってどういうこと?
想像してみてください。2人が同じ場所からスタートして、同じ方向にぐるぐる回ります。
- A君が池を2周したとき、B君はまだ1周と少ししか進んでいません
- A君がB君よりちょうど1周分(1200m)多く進んだら、また同じ場所に戻ってきます
- これが「次に出会う」瞬間です!
速さの差 = 80 – 60 = 20m/分
1200m縮めるのにかかる時間:
1200 ÷ 20 = 60分後
円周上(同じ方向)の公式
時間 = 円周 ÷ 速さの差
円周上(反対方向)の解き方【パターン⑤】
円周上を反対方向に進む問題です。
📝 例題
1周1200mの池の周りを、A君は分速80m、B君は分速60mで反対方向に進みます。
次に出会うのは何分後ですか?
📊 図で理解しよう
スタート時点:
🏃♂️A君(時計回り)
↓
●─────●
● 📍 ● ← 1周1200mの池
● ●
● ●
●─────●
↑
🚶♂️B君(反時計回り)
同じ地点から反対方向にスタート!
1分後:
🏃♂️A君は右に80m進む
🏃♀️B君は左に60m進む
→ 2人の間の距離は 80+60 = 140m 縮まる
🤔 考え方のポイント
反対方向に進むので、向かい合って近づいていくイメージです。
- A君とB君は合わせて毎分140mずつ近づく
- 池を半周ずつ進んで出会うわけではありません
- 2人が進んだ距離の合計が1200m(池1周分)になったときに出会います
速さの和 = 80 + 60 = 140m/分
1200mの距離を2人で縮めるのにかかる時間:
1200 ÷ 140 = 約8.6分後
円周上(反対方向)の公式
時間 = 円周 ÷ 速さの和
📊 円周上の2パターンまとめ
| パターン | 進む方向 | 使う公式 | 覚え方 |
|---|---|---|---|
| 同じ方向 | → → | 円周 ÷ 速さの差 | 追いかけっこ |
| 反対方向 | → ← | 円周 ÷ 速さの和 | 向かい合う |
旅人算を得意にする3つのコツ
1. まず図を描く
文章を読んだら、必ず図を描きましょう。
矢印で進む方向を書くだけでも理解が深まります。
2. 「速さの差」か「速さの和」かを見極める
- 同じ方向・追いかける → 速さの差
- 向かい合う・反対方向 → 速さの和
この判断ができれば、ほぼ正解です!
3. たくさん練習する
旅人算はパターン問題なので、数をこなせば必ず得意になります。
無料練習ツールで実践しよう
図解付きで楽しく学べる無料の計算ツールを作りました!
✨ 旅人算マスターの特徴
- ✨ 可愛いデザインで楽しく学べる
- 📊 図解で視覚的に理解できる
- 🎯 基礎から受験レベルまで対応
- 🏆 計算するたびにポイントがもらえる
旅人算マスター
楽しく学んでレベルアップ!
追いかけっこ!
ハイタッチ!
バイバイ~
グルグル~
追いかけっこ!
ハイタッチ!
バイバイ~
グルグル~
まとめ|旅人算は図とパターンで攻略
旅人算のポイントをおさらいします。
🎯 5つのパターン
- 追いつき算 → 速さの差
- 出会い算 → 速さの和
- 反向算 → 速さの和
- 円周上(同じ方向) → 速さの差
- 円周上(反対方向) → 速さの和
💡 解き方のコツ
- 必ず図を描く
- 「差」か「和」かを判断する
- パターンを覚える
旅人算は、一度理解すれば得点源になる単元です。
この記事と無料ツールを使って、しっかり練習していきましょう!
タグ:#旅人算 #小学生算数 #中学受験 #追いつき算 #出会い算 #算数解説



